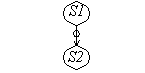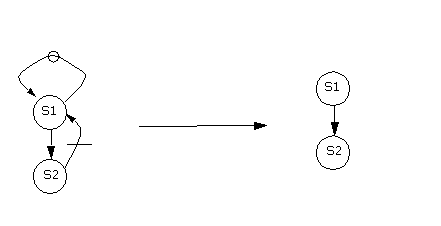Chapter 9:
DEPENDENCE-DRIVEN LOOP MANIPULATION
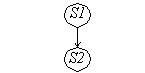
Flow Dependence (True Dependence)
S1 X=A+B
S2 C=X+1
Anti Dependence
S1 A=X+B
S2 X=C+D
Output Dependence
S1 X=A+B
. . .
S2 X=C+D
9.2 DEPENDENCE AND PARALLELIZATION (SPREADING)
C$OMP PSECTIONS
C$OMP SECTION
S1
S2
S3
C$OMP SECTION
S4
S5
S6
C$OMP END PSECTIONS
S7
C$OMP PSECTIONS
C$OMP SECTION
S8
S9
C$OMP SECTION
S10
S11
C$OMP END PSECTIONS
9.3 RENAMING
(To remove memory-related dependences)
S1 A=X+B
S2 X=Y+1
S3 C=X+B
S4 X=Z+B
S5 D=X+1
Use renaming.
S1 A=X+B
S2 X1=Y+1
S3 C=X1+B
S4 X2=Z+B
S5 D=X2+1
9.4 DEPENDENCES IN LOOPS
DO I=1,N
S1 A=B(I)+1
S2 C(I)=A+2
END DO
9.5 DEPENDENCES IN LOOPS (Cont.)
DO I =1,N
S1 X(I+1)=B(I)+1
S2 A(I)=X(I)
END DO
DO I=1,N
S1 X(I)=B(I)+1
S2 A(I)=X(I+1)+1
END DO
9.6 DEPENDENCE ANALYSIS
DO I=1,N
S1 X(F(I)) = B(I)+1
S2 A(I) = X(G(I))+2
END DO
We say that
IFF $ I
1
£ I
2
'
F (I
1
)=G(I
2)
[ALSO I
1
,I
2
e[1,N]]
We say that
IFF $ I
1
< I
2
'
F (I
2
)=G(I
1)
9.7 LOOP PARALLELIZATION AND VECTORIZATION
-
A loop whose dependence graph is cycle-free can be parallelized or vectorized.
e.g.
DO I=1,N
X(I)=B(I)+1
A(I)=X(I)+1
END DO
X(1:N)=B(1:N)+1 PARALLEL DO I=1,N
A(1:N)=X(1:N)+1 X(I)=B(I)+1
A(I)=X(I)+1
END PARALLEL DO
-
The reason is that if there are no cycles in the dependence graph, then there will be no races in the parallel loop.
9.8 ALGORITHM REPLACEMENT
-
Some program patterns occur frequently in programs. They can be replaced with a parallel algorithm.
e.g.
DO I=1,N
A(I)=A(I-1)+B(I)
END DO
A(1:N)=REC1N(B(1:N),A(0),N)
X=A(1)
DO I=2,N
IF(X.GT.A(I))X=A(I)
END DO
X=MIN(A(1:N))
9.9 LOOP DISTRIBUTION
-
To insulate these patterns, we can decompose loops into several loops, one for each strongly-connected component (p-block)in the dependence graph.
DO I=1,N
S1: A(I)-B(I)+C(I)
S2: D(I)=D(I-1)+A(I)
S3: IF(X.GT.A(I))THEN
S4 X=A(I)
ENDIF
END DO
DO I=1,N
A(I)=B(I)+C(I)
END DO
DO I=1,N
D(I)=D(I-1)+A(I)
END DO
DO I=1,N
IF (X.GT.A(I) THEN
X=A(I)
END IF
END DO
9.10 LOOP INTERCHANGING
-
The dependence information detremines whether or not the loop headers can be interchanged.
-
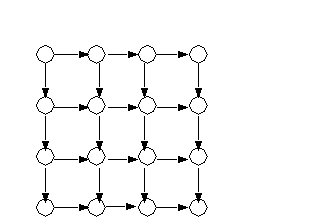
For example, the following loop headers can be interchanged
do i=1,n
do j=1,n
a(i,j) = a(i,j-1) + a(i-1,j)
end do
end do
-
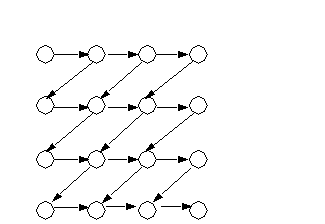
However, the headers in the following loop cannot be interchanged
do i=1,n
do j=1,n
a(i,j) = a(i,j-1) + a(i-1,j+1)
end do
end do
9.11 DEPENDENCE REMOVAL
-
Some cycles in the dependence graph can be eliminated by using elementary transformations.
Scalar Expansion:
DO I=1,N
S1: A=B(I)+1
S2: C(I)=A+D(I)
END DO
DO I=1,N
S1: A1(I)=B(I)+1
S2: C(I)=A1(I)+D(I)
END DO
A=A1(N)
9.12
Induction variable recognition
DO I=1,N
S1: J=J+2
S2: X(I)=X(I)+J
END DO
DO I=1,N
S1: J1=J+2*I
S2: X(I)=X(I)+J1
END DO
DO I=1,N
S1: J1(I)=J+2*I
S2: X(I)=X(I)+J1(I)
END DO
9.13 More about the DO to PARALLEL DO transformation
-
When the dependence graph inside a DO loop has no cross-iteration dependences, it can be transformed into a PARALLEL DO.
Example 1:
do i=1,n
S1: a(i) = b(i) + c(i)
S2: d(i) = x(i) + 1
end do
Example 2:
do i=1,n
S1: a(i) = b(i) + c(i)
S2: d(i) = a(i) + 1
end do
Example 3:
do i=1,n
S1: b(i) = a(i)
S2: do while b(i)**2-a(i).gt.epsilon
S3: b(i)=(b(i)+a(i)/b(i))/2.0
end do while
end do
-
When there are cross iteration dependences, but no cycles, do loops can be aligned to be transformed into DOALLs
Example 1:
do i=1,n
S1: a(i) = b(i) + 1
S2: c(i) = a(i-1)**2
end do
Ø
do i=0,n
S1: if i>0 then a(i) = b(i) + 1
S2: if i<n then c(i+1) = a(i)**2
end do
-
Sometimes we have to replicate to achieve alignment
Example 2:
do i=1,n
a(i) = b(i) + c(i)
d(i) = a(i) + a(i-1)
end do
óØ
do i=1,n
a(i) = b(i) + c(i)
a1(i) = b(i) + c(i)
d(i) = a1(i) + a(i-1)
end do
óØ
do i=0,n
if i>0 then a(i) =b(i) + c(i)
if i<n then a1(i+1)=b(i+1)+c(i+1)
d(i+1)=a1(i+1)+a(i)
end do
-
Need for replication could propagate.
Example 3:
do i=1,n
c(i) = 2 * f(i)
a(i) = c(i) + c(i-1)
d(i) = a(i) + a(i-1)
end do
Ø
do i=1,n
c(i) = 2 * f(i)
c1(i) = 2 * f(i)
c2(i) = 2 * f(i)
a(i) = c(i) + c1(i-1)
a1(i) = c1(i) + c2(i-1)
d(i) = a(i) + a1(i-1)
end do
-
The problem of finding the minimum amount of code replication sufficient to align a loop is NP-hard in the size of the input loop (Allen et al 1987)
-
To do alignment, we may need to do topological sort of the statements according to the partial order given by the dependence graph.
Example 4:
do i=1,n
S1: a(i) = b(i) + c(i-1)
S2: c(i) = d(i)
end do
-
Performing alignment without sorting first will clearly be incorrect in this case
-
Another method for eliminating cross-iteration dependences is to perform loop distribution.
Example:
do i=1,n
a(i) = b(i) + 1
c(i) = a(i-1) + 2
end do
Ø
do i=1,n
a(i) = b(i) + 1
end do
do i=1,n
c(i) = a(i-1) + 2
end do
9.14 Loop Coalescing for DOALL loops
-
A perfectly nested DOALL loop such as
doall i=1,n1
doall j=1,n2
doall k=1,n3
...
end doall
end doall
end doall
could be trivially transformed into a singly-nested loop with a tuple of variables as index:
doall (i,j,k) = (1..n1).c.(1..n2).c.(1..n3)
...
end doall
This coalescing transformation is convenient for scheduling and could reduce the overhead involved in starting DOALL loops.
If the loop construct has only one dimension, coalescing can be done by creating a mapping from a single index, say x into a multimensional index.
9.15 Cyclic Dependences -- DOPIPE
-
Assume a loop with two or more dependence cycles (strongly connected components or p-blocks)
-
The first approach developed for concurrentization of do loops is illustrated below:
do i=1,n
a(i) = b(i) + a(i-1)
c(i) = a(i) + c(i-1)
end do
ëØ
cobegin
do i=1,n
a(i) = b(i) + a(i-1)
post(s)
end do
//
do i=1,n
wait(s)
c(i) = a(i) + c(i-1)
end do
coend
i.e. to take a loop with two or more p-blocks such as: