Output Dependence
S1 X=A+B
. . .
S2 X=C+D
9.2 DEPENDENCE AND PARALLELIZATION (SPREADING)
C$OMP PSECTIONS
C$OMP SECTION
S1
S2
S3
C$OMP SECTION
S4
S5
S6
C$OMP END PSECTIONS
S7
C$OMP PSECTIONS
C$OMP SECTION
S8
S9
C$OMP SECTION
S10
S11
C$OMP END PSECTIONS
9.3 RENAMING
(To remove memory-related dependences)
S1 A=X+B
S2 X=Y+1
S3 C=X+B
S4 X=Z+B
S5 D=X+1
We say that
IFF $ I
1
< I
2
'
F (I
2
)=G(I
1)
9.7 LOOP PARALLELIZATION AND VECTORIZATION
-
A loop whose dependence graph is cycle-free can be parallelized or vectorized.
e.g.
DO I=1,N
X(I)=B(I)+1
A(I)=X(I)+1
END DO
X(1:N)=B(1:N)+1 PARALLEL DO I=1,N
A(1:N)=X(1:N)+1 X(I)=B(I)+1
A(I)=X(I)+1
END PARALLEL DO
-
The reason is that if there are no cycles in the dependence graph, then there will be no races in the parallel loop.
9.8 ALGORITHM REPLACEMENT
-
Some program patterns occur frequently in programs. They can be replaced with a parallel algorithm.
e.g.
DO I=1,N
A(I)=A(I-1)+B(I)
END DO
A(1:N)=REC1N(B(1:N),A(0),N)
X=A(1)
DO I=2,N
IF(X.GT.A(I))X=A(I)
END DO
X=MIN(A(1:N))
9.9 LOOP DISTRIBUTION
-
To insulate these patterns, we can decompose loops into several loops, one for each strongly-connected component (p-block)in the dependence graph.
DO I=1,N
S1: A(I)-B(I)+C(I)
S2: D(I)=D(I-1)+A(I)
S3: IF(X.GT.A(I))THEN
S4 X=A(I)
ENDIF
END DO
DO I=1,N
A(I)=B(I)+C(I)
END DO
DO I=1,N
D(I)=D(I-1)+A(I)
END DO
DO I=1,N
IF (X.GT.A(I) THEN
X=A(I)
END IF
END DO
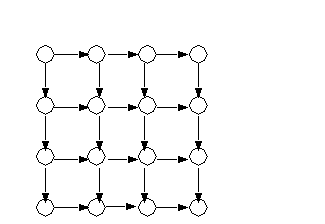
9.10 LOOP INTERCHANGING
-
The dependence information detremines whether or not the loop headers can be interchanged.
-
For example, the following loop headers can be interchanged
do i=1,n
do j=1,n
a(i,j) = a(i,j-1) + a(i-1,j)
end do
end do
-
However, the headers in the following loop cannot be interchanged
do i=1,n
do j=1,n
a(i,j) = a(i,j-1) + a(i-1,j+1)
end do
end do
Scalar Expansion:
DO I=1,N
S1: A=B(I)+1
S2: C(I)=A+D(I)
END DO
DO I=1,N
S1: A1(I)=B(I)+1
S2: C(I)=A1(I)+D(I)
END DO
A=A1(N)
9.12
Induction variable recognition
DO I=1,N
S1: J=J+2
S2: X(I)=X(I)+J
END DO
DO I=1,N
S1: J1=J+2*I
S2: X(I)=X(I)+J1
END DO
DO I=1,N
S1: J1(I)=J+2*I
S2: X(I)=X(I)+J1(I)
END DO
9.13 More about the DO to PARALLEL DO transformation
-
When the dependence graph inside a DO loop has no cross-iteration dependences, it can be transformed into a PARALLEL DO.
Example 1:
do i=1,n
S1: a(i) = b(i) + c(i)
S2: d(i) = x(i) + 1
end do
Example 2:
do i=1,n
S1: a(i) = b(i) + c(i)
S2: d(i) = a(i) + 1
end do
Example 3:
do i=1,n
S1: b(i) = a(i)
S2: do while b(i)**2-a(i).gt.epsilon
S3: b(i)=(b(i)+a(i)/b(i))/2.0
end do while
end do
-
When there are cross iteration dependences, but no cycles, do loops can be aligned to be transformed into DOALLs
Example 1:
do i=1,n
S1: a(i) = b(i) + 1
S2: c(i) = a(i-1)**2
end do
Ø
do i=0,n
S1: if i>0 then a(i) = b(i) + 1
S2: if i<n then c(i+1) = a(i)**2
end do
-
Sometimes we have to replicate to achieve alignment
Example 2:
do i=1,n
a(i) = b(i) + c(i)
d(i) = a(i) + a(i-1)
end do
óØ
do i=1,n
a(i) = b(i) + c(i)
a1(i) = b(i) + c(i)
d(i) = a1(i) + a(i-1)
end do
óØ
do i=0,n
if i>0 then a(i) =b(i) + c(i)
if i<n then a1(i+1)=b(i+1)+c(i+1)
d(i+1)=a1(i+1)+a(i)
end do
-
Need for replication could propagate.
Example 3:
do i=1,n
c(i) = 2 * f(i)
a(i) = c(i) + c(i-1)
d(i) = a(i) + a(i-1)
end do
Ø
do i=1,n
c(i) = 2 * f(i)
c1(i) = 2 * f(i)
c2(i) = 2 * f(i)
a(i) = c(i) + c1(i-1)
a1(i) = c1(i) + c2(i-1)
d(i) = a(i) + a1(i-1)
end do
-
The problem of finding the minimum amount of code replication sufficient to align a loop is NP-hard in the size of the input loop (Allen et al 1987)
-
To do alignment, we may need to do topological sort of the statements according to the partial order given by the dependence graph.
Example 4:
do i=1,n
S1: a(i) = b(i) + c(i-1)
S2: c(i) = d(i)
end do
-
Performing alignment without sorting first will clearly be incorrect in this case
-
Another method for eliminating cross-iteration dependences is to perform loop distribution.
Example:
do i=1,n
a(i) = b(i) + 1
c(i) = a(i-1) + 2
end do
Ø
do i=1,n
a(i) = b(i) + 1
end do
do i=1,n
c(i) = a(i-1) + 2
end do