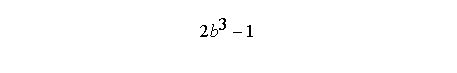Fortran is not a flower, but a weed. It is hardy, occasionally blooms, and grows in every computer. (A. Perlis)
-
In 1954 a project was begun under the leadership of John Backus at IBM to develop an "automatic programming" system that would convert programs written in a mathematical notation to machine instructions for the IBM 704 computer.
-
Many were skeptical that the project would be successful. It was necessary for the program produced by the compiler to be almost as efficient as that produced by a good assembly language programmer.
-
First compiler in 1957. Quite successful.
-
Several ANSI standards: 1966 (Fortran 66), 1978 (Fortran 77), 1990 (Fortran 90).
4.1 Source form
Traditionally, Fortran statements had a fixed format:
Columns 1-5: label (a number)
Column 6: Continuation mark
Columns 7-72: statement
A C in column 1 indicates that the whole line is a comment.
Examples of Fortran statements:
C This is a comment line
10 I = 1
DO 15 J = I, 10
A(J) = 0
15 CONTINUE
C Now a very long statement
CALL SUBSUB(X,Y,...
* Q,W)
Free format is accepted by most Fortran compilers today.
Up to 132 characters per line are allowed in Fortran 90.
An ampersand indicates line continuation. For example:
CALL SUBSUB(X,Y,... &
Q,W)
The exclamation mark is often used to indicate the beginning of a comment:
i = 1 ! This is a comment
Lower case letters are considered equal to the corresponding upper case letters except inside a character constant.
Thus,
aBc = 1
is the same as
ABC = 1
But
'aBc'
is not equal to
'ABC'
4.2 Data types
There are six basic data types in Fortran 77:
-
Integer
-
Real
-
Double precision
-
Complex
-
Logical
-
Character
Integer and real constants are similar to those in C.
Double precision constants are similar to real constants with exponents, but a D is used instead of an E:
1.D0, 3.527876543D-4
Complex constants are pairs of reals or integers enclosed in parentheses and separated by a comma. The first number is the real part and the second the imaginary part:
(1.23 , 23e1)
Logical constants are .TRUE. and .FALSE.
The form of a character constant is an apostrophe, followed by a nonempty string of characters, followed by an apostrophe. Two consecutive apostrophes represent the apostrophe.
'abc' 'a''b'
4.3 Variables
Variables in Fortran 77 start with a letter, contain only letters and digits, and are no more than six characters long. In Fortran 90 up to 31 characters are allowed and the underscore _ can form part of the variable name.
The type of variables is specified either explicitly in a type declaration statement or is implicit. Examples of type declaration statements:
real a,b,c(10,10)
integer i,j,k(100)
double precision ...
complex ...
logical q, p r
character s,t * 5,u(20,20)
character * 10 v, w, y
The * num in the character statement specifies the length of the variable in number of characters. It applies to the whole list if it appears after the character keyword, or to the variable if it appears after a variable name.
A scalar variable does not have to be declared in Fortran. The first letter of an undeclared variable indicates its type. Variables starting with letter I thorough N (INteger) are of type integer variables. All other undeclared variables are of type real. This default option can be changed with the IMPLICIT statement.
An array declarator is a variable name followed by a specification of the dimensions. The dimension specification has the form ( d1 , d2 ,...)
where
di
s represent the size of each dimension
. In the main program the dimensions are specified using integer constants. They could be a single integer, say n, meaning that the possible subscripts are from one to n. Also, they could be a pair of integers, say m:n, meaning that the values of the subscripts for that dimension have to be between n and m.
A declarator can also appear in a dimension statement, Thus:
real a
dimension a(10,10), b(5:15,5)
is equivalent to ( b is implicitly declared as real)
real a(10,10), b(5:15,5)
Note: Dimension declarators for subroutine parameters can contain variables or can be the special character *.
4.4 Expressions
Expressions in Fortran can be arithmetic, relational, logical and character.
Arithmetic expressions are similar to those in C, except that in Fortran there is an exponentiation operator (**) which has the highest precedence. Thus, the right-hand side expression in the statement
a = 2*b**3-1
has the value:
Implicit type conversion is also similar to C.
The only character operator is concatenation (//):
'AB' // 'DE'
Relation operators compare the values of expression and produce a logical value of true or false. The relation operators have lower precedence than arithmetic operators.
The relation operators are:
.LT. Less than
.LE. Less than or equal to
.EQ. Equal to
.NE. Not equal to
.GT. Greater than
.GE. Greater than or equal to
For example,
if (a*b .gt. c-1) then ...
logical q
q = t-1 .gt. 5
if (q) then ...
The logical operators are:
.NOT. Logical negation
.AND. Logical Conjunction
.OR. Logical inclusive disjunction
.EQV. Logical equivalence
.NEQV. Logical nonequivalence
4.5 Fortran statements
We will only discuss a few of the statements:
-
GOTO statement. (e.g GO TO 150)
-
IF statement.
if (a.gt. 5) a = 5
if (a.gt. 5) then
a=5
b=1
end if
if (a.gt. 5) then
a=5
b=1
else
b=2
go to 17
end if
-
DO statement. Iterative statement.
do 10 i=1,n
do 15 j=1,n
a(i,j) = 0
15 continue
10 continue
do 10 i=1,n
do 10 j=1,n
10 a(i,j) = 0
do i=1,n ! this form is not accepted
! by all compilers
do j=1,n
a(i,j) = 0
end do
end do
do 2 i=1,n,2 !This do loop updates
!elements 1, 3, 5, ...
b(i) = 1
2 continue
-
CALL statement. For subroutine invocation:
call subsub(a, b(1,5),35,.true.)
4.6 Program Units
A Fortran program always includes a Main Program and may include subroutines and functions. The generic name for the main program, subroutines, and functions is program unit.
There are three classes of functions in Fortran: intrinsic functions, statement functions and external functions.
All functions are referenced in the same way. A function reference is always within an expression and has the form
fun (a,a,...)
where the a's are the actual arguments.
For example, the following expression contains two references to functions:
sin(x) + root(f,a,b) + y
In this example, sin and root are function names and x, f, a, and b are actual arguments. The actual arguments can be variables, constant, or function/subroutine names.
Fortran includes a number of pre-defined intrinsic functions such as sin, cos, max, sign, etc. These are described in any Fortran manual.
Statement functions are declared at the beginning of the program. The declaration has the form:
fun ( d, d, ...) = e
where the d's are dummy arguments and e is an expression that may contain constants, dummy arguments, program variables and references to any type of function.
The type of the value returned by the statement function depends on the type associated with the function name. The type is assigned using either type declaration statements or, if the function name is not declared, the implicit rules described above for variables. An example of a statement function is:
real mpyadd, b(100)
...
mpyadd(x,y,z) = x*y + z + 2 + sin(x)
...
y = mpyadd(a,b(5),1.0)
Notice that the variable y in the last assignment statement is different from the dummy argument in the statement function. In fact, dummy arguments in a statement function have a scope of that statement.
External functions can be compiled separately from the main program. They may include several executable statements. Their overall form is:
<type> FUNCTION fun (d ,d, ...)
Declarations and executable statements
END
The name of the function (fun) must appear as a variable within the subprogram. The variable must be defined on every execution of the function, and its value at the end of the subprogram is the value returned by the function.
The type of the (value returned by) function is determined either using the implicit rules or by the <type> specified in the function header.
4.7 I/O statements
There are many different ways of reading and writing in Fortran.
The simplest forms are:
read *,
iolist
print *,
iolist
Here, the read and write operate on the standard input and standard output.
The data is written as a sequence on constants that take the same form they would take within Fortran program. They should be separated by spaces or commas.
Type conversion is follows the same rules of assignment statements.
Each print starts a new line.
Each read starts on the next record.
A read, processes as many records as necessary to assign values to the variables in its iolist.
iolist is a sequence of variables perhaps surrounded by implicit loops of the form
(variable, index=l,u,s).
For example:
read *, n,(a(i),i=1,n), ((b(i,j),i=1,n),j=1,n)
4.8 Examples
subroutine mprove(a,alud,n,np,indx,b,x)
parameter (nmax=100)
dimension a(np,np), alud(np,np), indx(n), b(n), x(n), r(nmax)
real*8 sdp
do i=1,n
sdp=-b(i)
do j=1,n
sdp=sdp+dble(a(i,j))*dble(x(j))
end do
r(i)=sdp
end do
call lubksb(alud,n,np,indx,r)
do i=1,n
x(i)=x(i)-r(i)
end do
return
end
function rtflsp(func,x1,x2,xacc)
parameter (maxit=30)
fl=func(x1)
fh=func(x2)
if(fl*fh.gt.o.) pause `root must be bracketed for false position.'
if(fl.lt.o.) then
xl=x1
xh=x2
else
xl=x2
xh=x1
swap=fl
fl=fh
fh=swap
endif
dx=xh-xl
do j=1,maxit
rtflsp=xl+dx*fl/(fl-fh)
f=func(rtflsp)
if(f.lt.o.) then
del=xl-rtflsp
xl=rtflsp
fl=f
else
del=xh-rtflsp
xh=rtflsp
fh=f
endif
dx=xh-xl
if(abs(del).lt.xacc.or.f.eq.o.)return
end do
pause `rtflsp exceed maximum iterations'
end
-
Triplet notation:
Sections of arrays are identified in Fortran 90 using triplets of the form
l:u:s
. A triplet represent the sequence of subscripts
l, l+s, l+2*s,...,l+m*s
l+(m+1)s > u (if s l)
l+(m+1)s < u (if s £ l)
For example, the section A(3:5,2,1:2) of an array A is the array of shape (3,2):
A(3,2,1) A(3,2,2)
A(4,2,1) A(4,2,2)
A(5,2,1) A(5,2,2)
If l is omitted, the lober bound for the array is assumed. If u is omitted, the upper bound is assumed. If s is omitted, 1 is assumed. The stride s cannot be 0
-
Expressions in Fortran 90 may contain array sections, specified using triplets, or complete arrays identified by the name of the array without any subscripts.
For example, consider the arrays a, b and c declared as follows:
dimension a(100,100) b(100,100),c(100,100)
c = a + b
a(1:100, 2) = 0
assigns 0 to the second column of a. An identical function is performed by the following three statements.
a(:100,2) = 0
a(1:,2) = 0
a(:,2) = 0
a(51:100,4) = b(1:50,4) * c(30,31:80)
a(51:100,4) = a(50:99,4) + 1
-
The rank of an array is the number of dimensions.
-
The shape of an array is determined by its rank and its extent in each dimension.
-
All the objects in an expression or assignment statement must be conformable. Two arrays are conformable if they have the same shape. A scalar is conformable with any array.
-
Any intrinsic operation defined for scalar objects may be applied to conformable objects. Such operations are performed element-by-element to produce a resultant array conformable with the array operands.
-
The masked array assignment is used to perform selective assignment to arrays. For example, in the statement
where(temp>0)temp = temp - reduce_temp
In the following compound statement,
where(pressure<=0)
pressure = pressure + inc_pressure
temp = temp - 5.0
elsewhere
raining = .true.
end where
the array
pressure
in modified only where it is <= 1. Also, the array
temp
is modified in the corresponding locations (i.e. in the same locations as pressure). Finally, the array
raining
is assigned
.true.
only in the locations that correspond to those element of
pressure
which are > 1.
-
The mask of the
where
statement is like another operator on the right-hand side of all the assignment statements in the body of the
where
statement and therefore has to be conformable to the right-hand side expression and to the array on the left-hand side.
-
There are a collection of intrinsic functions designed to operate on arrays. These will be described as needed.
6.1 Introduction
OpenMP is a collection of compiler directives, library routines, and environment variables that can be used to specify shared memory parallelism.
This collection has been designed with the cooperation of many computer vendors including Intel, HP, IBM, and SGI. So, it is likely to become the standard (and therefore portable) way of programming SMPs.
The Fortran directives have already been defined and similar extensions for C and C++ are underway.
6.2 The
PARALLEL
directive
The
parallel
/
end parallel
directive pair defines a parallel region and constitutes as parallel construct.
An OpenMP program begins execution as a single task, called the
master thread. When a parallel construct is encountered, the master thread creates a team of threads. The statements enclosed by the parallel construct, including routines called from
within the enclosed construct, are executed in parallel by each thread in the team.
At the end of the parallel construct the threads in the team synchronize and only the master thread continues execution.
The general form of this construct is:
C$omp parallel [parallel-clause[[,]parallel-clause] ...]
parallel region
C$omp end parallel
There are several classes of parallel-clauses. Next, we discuss the private(
list
)clause.
All variables are assumed to be shared by all tasks executing the parallel region. However, there will be a separate copy of each variable listed in a
private
clause for each task. There will also be an additional copy of the variable that can be accessed outside the parallel region.
Variables defined as private are undefined for the thread entering the construct and are also undefined for the thread on exit from a parallel construct.
As an example, consider the following code segment
c = sin (d)
forall i=1 to n
a(i) = b(i) + c
end forall
e = a(20)+ a(15)
A simple OpenMP implementation would take the form
c = sin(d)
c$omp parallel private(i,il,iu)
call get_limits(n,il,iu,
* omp_get_num_threads(),
* omp_get_thread_num())
do i=il,iu
a(i) = b(i) + c
end do
c$omp end parallel
e = a(20) + a(15)
Notice that the first statement can be incorporated into the parallel region. In fact,
c
can be declared as private assuming it is never used outside the loop.
c$omp parallel private(c,i,il,iu)
c= sin(d)
call get_limits(n,il,iu,
* omp_get_num_threads(),
* omp_get_thread_num())
do i=il,iu
a(i) = b(i) + c
end do
c$omp end parallel
e = a(20) + a(15)
6.3 The
BARRIER
directive
To incorporate
e
into the parallel region it is necessary to make sure that
a(20)
and
a(15)
have been computed before the statement executes.
This can be done with a
barrier
directive which synchronizes all the threads in the enclosing
parallel
region. When encountered, each thread waits until all the others in that team have reached this point.
c$omp parallel private(c,i,il,iu)
c = sin(d)
call get_limits(n,il,iu,
* omp_get_num_threads(),
* omp_get_thread_num())
do i=il,iu
a(i) = b(i) + c
end do
c$omp barrier
e = a(20) + a(15)
c$omp end parallel
6.4 The
PSINGLE
directive
Finally, since
e
is shared, it is not a good idea for all tasks in the team to execute the last assignment statement. There will be several redundant assignments all competing for access to the single memory location. Only one task needs to execute the assignment.
This can be accomplished with the
psingle
directive:
c$omp parallel private(c,i,il,iu)
c = sin(d)
call get_limits(n,il,iu,
* omp_get_num_threads(),
* omp_get_thread_num())
do i=il,iu
a(i) = b(i) + c
end do
c$omp barrier
c$omp psingle
e = a(20) + a(15)
c$omp end psingle nowait
c$omp end parallel
The
psingle
directive has the following syntax:
c$omp psingle [single-clause[[,]single-clause] ...]
block
c$omp end psingle [nowait]
This directive specifies that the enclosed region of code is to be executed by one and only one of the tasks in the team.
Tasks in the team not executing the
psingle
block wait at the
end psingle
, unless
nowait
is specified. In this case, there is no need for this implicit barrier since one already exists at the
end parallel
directive.
One of the two
single-clauses
is private(
list
).
A better example of
psingle
:
subroutine sp_1a(a,b,n)
c$omp parallel private(i)
c$omp pdo
do i=1,n
a(i)=1.0/a(i)
end do
c$omp psingle
a(1)=min(a(1),1.0)
c$omp end psingle
c$omp pdo
do i=1,n
b(i)=b(i0/a(i)
c$omp end pdo nowait
c$omp end parallel
end
6.5 The
PDO
directive
A simpler way to write the previous code uses the
pdo
directive:
c$omp parallel private(c,i,il,iu)
c = sin(d)
c$omp pdo schedule(static)
do i=1,n
a(i) = b(i) + c
end do
c$omp end pdo
c$omp psingle
e = a(20) + a(15)
c$omp end psingle nowait
c$omp end parallel
The
pdo
directive specifies that the iteration s of the immediately following do loop must be executed in parallel.
The syntax of the
pdo
directive is as follows:
c$omp pdo [pdo-clause[[,]pdo-clause] ...]
do loop
c$omp end pdo [nowait]
There are several
pdo clauses
including
private
and
schedule
.
The schedule could assume other values including
dynamic.
The nowait clause eliminates the implicit barrier at the end pdo directive. In the previous example, the nowait clause should not be used.
An example of
pdo
with the
nowait
directive is
subroutine pdo_2(a,b,c,d,m,n)
real a(n,n),b(n,n),c(m,m), d(m,m)
c$omp parallel private(i,j)
c$omp pdo schedule(dynamic)
do i=2,n
do j=1,i
b(j,i)=(a(j,i)+a(j,i+1))/2
end do
end do
c$omp end pdo nowait
c$omp pdo schedule(dynamic)
do i=2,m
do j=1,i
d(i,j)=(c(j,i)+c(j,i-1))/2
end do
end do
c$omp end pdo nowait
c$omp end parallel
end
6.6 The
PARALLEL DO
directive
An alternative to the
pdo
is the
parallel do
directive which is no more than a shortcut for a
parallel
directive containing a single
pdo
directive.
For example, the following code segment
c$omp parallel private(i)
c$omp pdo schedule(dynamic)
do i=1,n
b(i)=(a(i)+a(i+1))/2
end do
c$omp end pdo nowait
c$omp end parallel
end
could be rewritten
c$omp parallel do
c$omp & private(i)
c$omp& schedule(dynamic)
do i=1,n
b(i)=(a(i)+a(i+1))/2
end do
c$omp end parallel do
end
And the routine
pdo_2
can be rewritten as follows:
subroutine pdo_2(a,b,c,d,m,n)
real a(n,n),b(n,n),c(m,m), d(m,m)
c$omp parallel do
c$omp& private(i,j)
c$omp& schedule(dynamic)
do i=2,n
do j=1,i
b(j,i)=(a(j,i)+a(j,i+1))/2
end do
end do
c$omp end parallel do
c$omp parallel do
c$omp& private(i,j)
c$omp& schedule(dynamic)
do i=2,m
do j=1,i
d(i,j)=(c(j,i)+c(j,i-1))/2
end do
end do
c$omp end parallel do
end
There are two disadvantages to this last version of pdo_2:
-
There is a barrier at the end of the first loop.
-
There are two parallel regions. There is overhead at the beginning of each.
6.7 The
PSECTIONS
directive
An alternative way to write the
pdo_2
routine is:
subroutine pdo_2(a,b,c,d,m,n)
real a(n,n),b(n,n),c(m,m), d(m,m)
c$omp parallel private(i,j)
c$omp psections
c$omp psection
do i=2,n
do j=1,i
b(j,i)=(a(j,i)+a(j,i+1))/2
end do
end do
c$omp psection
do i=2,m
do j=1,i
d(i,j)=(c(j,i)+c(j,i-1))/2
end do
end do
c$omp end psections nowait
c$omp end parallel
end
The
psections
directive specifies that the enclosed sections of code are to be divided among threads in the team. Each section is executed by one thread in the team. Its syntax is as follows:
c$omp psections[sections-clause[[,]sections-clause] ...]
[c$omp psection]
block
[[c$omp psection
block
]
.
.
.]
c$omp end psections [nowait]
Chapter 7. Parallel Loops in OpenMP
Parallel loops are the most frequently used constructs for scientific computing in the shared-memory programming model.
In this chapter we will discuss omp parallel loops.
We begin with the definition of race.
7.1 Races
We say that there is a race when there are two memory references taking place in two different tasks such that
-
They are not ordered
-
They refer to the same memory location
-
One of them is a memory write (store).
For example, in the following code there is a race due to the two accesses to
a:
c$omp parallel sections
c$omp psection
...
a = x + 5
...
c$omp psection
...
y = a + 1
...
c$omp end parallel sections
Another example of a race is:
c$omp parallel
...
if (omp_get_thread_num().eq.0) a=x+5
... [no
omp
directive here]
if (omp_get_thread_num().eq.1) a=y+1
...
c$omp end parallel
However, there is no race in the following code because the two references to
a
are ordered by the barrier.
c$omp parallel
...
if (omp_get_thread_num().eq.0) a=x+5
...
c$omp barrier
...
if (omp_get_thread_num().eq.1) a=y+1
...
c$omp end parallel
Another example of a race is:
c$omp parallel do
do i=1,n
...
a = x(i) + 1
...
end do
c$omp end parallel do
Here,
a
is written in all iterations. There is a race if there are at least two tasks executing this loop. (It is ok to execute an OpenMP program with a single processor)
Another example is:
c$omp parallel do
do i=1,n
...
a(i) = a(i-1) + 1
...
end do
Here, if at least two tasks cooperate in the execution of the loop, some pair of consecutive (say iterations j and j+1) iterations will be executed by different tasks.
Then, one of the iterations will write to an array element (say
a(j)
in iteration
j
) and the other will read the same element in the next iteration.
Sometimes it is desirable to write a parallel program with races. But most often it is best to avoid races.
In particular, unintentional races may lead to difficult to detect bugs.
Thus, if
a
has the value 1 and
x
the value 3 before the following parallel section starts,
y
could be assigned either 2 or 9. This would be a bug if the programmer wanted
y
to get the value 9. And the bug could be very difficult to detect if, for example,
y
were to get the value 2 very infrequently.
c$omp parallel sections
c$omp section
...
a = x + 5
...
c$omp section
...
y = a + 1
...
c$omp end parallel sections
7.2 Race-free parallel loops
Next, we present several forms of parallel loops. In each case, a conventional (sequential) version of the loop will be presented first.
This does not mean that parallel loops can be written only by starting with a conventional loop. However, the most important forms of parallel loops can be easily understood when presented in the context of conventional loops.
The first form of parallel loop can be obtained quite simply. A conventional loop can be transformed into parallel form by just adding a
parallel loop
directive if the resulting parallel loop contains no races between any pair of iterations.
An example is the loop
do i=1,n
a(i) = b(i) +1
end do
Notice that this loop computes the vector operation
a(1:n)=b(1:n)+1
More complex loops can also be directly transformed into parallel form. For example:
do i=1,n
if (c(i) .eq. 1) then
do while (a(i) .gt. eps)
a(i) = x(i) - x(i-1) / c
end do
else
do while (a(i) .lt. upper)
a(i) = x(i) + y(i+1) * d
end do
end if
end do
Notice that although consecutive iterations access the same element of
x,
there is no race because both accesses are reads.
7.3 Privatization
Sometimes the transformation into parallel form requires the identification of what data should be declared as
private
.
For example, consider the following loop:
do i=1,n
x = a(i)+1
b(i) = x + 2
c(i) = x ** 2
end do
This loop would be fully parallel if it were not for
x
which is stored and read in all iterations.
One way to avoid the race is to eliminate the assignment to
x by forward substituting a(i)+1:
do i=1,n
b(i) = (a(i)+1) + 2
c(i) = (a(i)+1) ** 2
end do
A simpler way is to declare
x
as private:
c$omp parallel do private(i,x)
do i=1,n
x = a(i)+1
b(i) = x + 2
c(i) = x ** 2
end do
In general, a scalar variable can be declared
private
if
-
It is always assigned before it is read in every iteration of the loop, and
-
It is never used again, or it is reassigned before used again after the loop completes.
Sometimes it is necessary to privatize arrays. For example, the loop
do i=1,n
do j=1,n
y(j) = a(i,j) + 1)
end do
...
do k=2,n-1
b(i,j) = y(j) ** 2
end do
end do
can be directly parallelized if vector
y
is declared
private.
An array can be declared private if
-
No element of the array is read before it is assigned within the same iteration of the loop.
-
Any array element used after the loop completed is reassigned before it is read.
An important case arises when the variable to be privatized is read after the loop completes without reassignment.
For example
do i=1,n
x = a(i)+1
b(i) = x + 2
c(i) = x ** 2
end do
...=x
One way to solve this problem is to "peel off" the last iteration of the loop and then parallelize:
c$omp parallel do private(i,x)
do i=1,n-1
x = a(i)+1
b(i) = x + 2
c(i) = x ** 2
end do
x=a(n)+1
b(n)=x+2
c(n)=x+2
An equivalent, but simpler approach is to declare
x
as
lastprivate.
c$omp parallel do private(i) lastprivate(x)
do i=1,n
x = a(i)+1
b(i) = x + 2
c(i) = x ** 2
end do
Variables in lastprivate are private variables; however, in addition, at the end of the do loop, the thread that executes the last iteration updates the version of the variable that exists outside the loop.
If the last iteration does not assign a value to the entire variable, the variable is undefined after the loop.
For example, if
c(n) > 5
in the loop:
c$omp parallel do private(i) lastprivate(x)
do i=1,n
if (c(i).lt.5) then
x=b(i)+1
a(i)=x+x**2
end if
end do
then
x
would not be defined after the loop.
Similarly, if the private variable is a vector, only the elements assigned in the last iteration will be defined. (in KAI's version, the elements not assigned in the last iteration are 0).
For example, the program:
real a(100),b(100),c(100)
do i=1,100
a(i)=1
end do
do i=1,100
b(i)=3
end do
print *,a(1),a(2)
b(1)=1
c$omp parallel do lastprivate(a)
do i=1,100
do j=1,100
if (b(j).lt.3) then
a(j)=3
c(j)=a(j)
end if
end do
end do
print *,a(1),a(2)
end
prints
1.000000 1.00000
3.000000 0.
A similar situation arises when a private variable needs to be initialized with values from before the loop starts execution. Consider the loop:
do i=1,n
do j=1,i
a(j) = calc_a(j)
b(j) = calc_b(i,j)
end do
do j=1,n
x=a(j)-b(j)
y=b(j)+a(j)
c(i,j)=x*y
end do
end do
To parallelize this loop,
x
,
y
,
a
and
b
should be declared private. However, in iteration i the value of
a(i+1), a(i+2),...,a(n)
and of
b(i+1),b(i+2),...,b(n)
are those assigned before the loop starts.
To account for this,
a
and
b
should be declared as
firstprivate.
c$omp parallel do private(i,j,x,y)
c$omp& firstprivate(a,b)
7.4 Induction variables
Induction variables appear often in scientific programs. These are variables that assume the values of an arithmetic sequence across the iterations of the loop:
For example, the loop
do i=1,n
j = j + 2
do k=1,j
a(k,j) = b(k,j) + 1
end do
end do
cannot be directly transformed into parallel form because the satement
j=j+2 produces a race. And j cannot be privatized because it is read before it is assigned.
However, it is usually easy to express induction veriables as a function of the loop index. So, the previous loop can be tranformed into:
do i=1,n
m=2*i+j
do k=1,m
a(k,m) = b(k,m) + 1
end do
end do
In this last loop,
m
can be made private and the loop directly tranformed into parallel form.
If the last value of variable
j
within the loop is used after the loop completes, it is necessary to add the statement
j=2*n+j
immediately after the loop to set the variable
j
to its correct value.
Most induction variables are quite simple, like the one in the previous example. However, in some cases a more involved formula is necessary to represent the induction variable as a function of the loop index:
For example consider the loop:
do i=1,n
do j=1,m
k=k+2
a(k)=b(i,j)+1
end do
end do
The only obstacle for the parallelization of loop
i
is the induction variable
k
. Notice that no two iterations assign to the same element of array
a
because
k
always increases from one iteration to the next.
The formula for
k
is somewhat more involved than the formula of the previos example, but still is relatively simple:
c$omp parallel do private(i,j)
do i=1,n
do j=1,m
a(2*(m*(i-1)+j)+k)=b(i,j)+1
end do
end do
k=2*n*m+k
As a final example, consider the loop:
do i=1,n
j=j+1
a(j)= b(i)+1
do k=1,i
j=j+1
c(j)=d(i,k)+1
end do
end do
Here, again, only the induction variable,
j,
causes problems. But now the formulas are somewhat more complex:
c$omp parallel do private(i,k)
do i=1,n
a(i+i*(i-1)/2)= b(i)+1
do k=1,i
c(i+i*(i-1)/2+k)=d(i,k)+1
end do
end do
j=n+n*(n+1)/2
Sometimes, it is necessary to do some additional transformations to remove induction veriables. Consider the following loop:
j=n
do i=1,n
b(i)=(a(j)+a(i))/2.
j=i
end do
Variable
j
is called a
wraparound
variable of first order. It is called first order because only the first iteration uses a value of
j
from outside the loop. A wraparound variable is an induction variable whose value is carried from one iteration to the next.
The way to remove the races produced by
j
is to peel off one iteration, move the assignment to
j
from one iteration to the top of the next iteration (notice that now j must be assigned
i-1
), and then privatize :
j=n
if (n>=1) then
b(1)=(a(j)+a(1))/2.
c$omp parallel do private (i),lastprivate(j)
do i=2,n
j=i-1
b(i)=(a(j)+a(i))/2.
end do
end if
Notice that the if statement is necessary to make sure that the first iteration is executed only if the original loop would have executed it.
Alternatively, the wraparound variable could be an induction variable. The transformation in this case is basically the same as above except that the induction variable has to be expressed in terms of the loop index first.
Consider the loop:
j=n
do i=1,n
b(i)=(a(j)+a(i))/2.
j=j+1
end do
As we just said, we first replace the right hand side of the assignement to
j
with an expression involving
i.
j=n
do i=1,n
b(i)=(a(m)+a(i))/2.
m=i+j
end do
j=n+j
Notice that we changed the name of the variable within the loop to be able to use the value of
j
coming from outside the loop.
We can now proceed as above to obtain:
j=n
if (n>=1) then
b(1)=(a(j)+a(i))/2.
c$omp parallel do private (i,m)
do i=2,n
m=i-1+j
b(i)=(a(m)+a(i))/2.
end do
j=n+j !this has to be inside the if
end if
7.5 Ordered sections.
Sometimes the only way to avoid races is to execute the code serially. Consider the looP:
do i=1,n
a(i)=b(i)+1
c(i)=sin(c(i-1))+a(i)
d(i)=c(i)+d(i-1)**2
end do
Although there is no clear way to avoid races in this loop, we could execute in parallel the first statement. In fact, we can in this case transform the loop into:
c$omp parallel do
do i=1,n
a(i)=b(i)+1
end do
do i=1,n
c(i)=sin(c(i-1))+a(i)
d(i)=c(i)+d(i-1)**2
end do
However, there is a way to improve the performance of the whole loop with the
ordered
directive whose syntax is as follows:
c$omp ordered [(name
)]
block
c$omp end ordered [(name
)]
The interleaving of the statements in the ordered sections of different iterations are identical to that of the sequential program. Ordered sections without a name are all assumed to have the same name.
Thus, the previous loop can be rewritten as:
c$omp parallel do
do i=1,n
a(i)=b(i)+1
c$omp ordered (x)
c(i)=sin(c(i-1))+1
c$omp end ordered(x)
c$omp ordered (y)
d(i)=c(i)+d(i-1)**2
c$omp end ordered (y)
end do
Thus, we have two ways of executing the loop in parallel. Assuming n=12, and four processors, the following time lines are feasible:
Notice that now no races exist because accesses to the same memory location are always performed in the same order.
Ordered sections may need to include more than one statement. For example, in the loop:
do i=1,n
...
a(i)=b(i-1)+1
b(i)=a(i)+c(i)
...
end do
the possibility of races would not be avoided unless both statements are made part of the same ordered section.
It is important to make the ordered sections as small as possible because the overall execution time depends on the size of the longest ordered section.
7.6 Execution time of a
parallel do
when
ordered
sections have constant execution time.
c$omp parallel do
do i=1,n
c$omp ordered (a)
aa = ...
c$omp end ordered (a)
c$omp ordered (b)
...
c$omp ordered (c)
...
c$omp ordered (d)
...
c$omp ordered (e)
...
end do
-
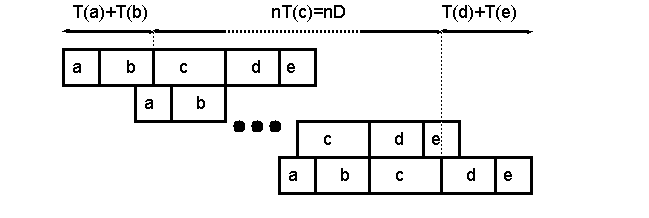
Assume its execution time lines have the following form:
which, in terms of performance, is equivalent to the following time lines:
where a constant delay D between the start of consecutive iterations is evident. This delay is equal to the time of the longest ordered section (i.e., D=T(c) in this case).
-
The execution time of the previous loop using n processors is:
T(a)+T(b)+nT(c)+T(d)+T(e)
-
In general the execution time when there are as many processors as iterations is
nD+(B-D)=(n-1)D+B
7.6 Critical Regions and Reductions
Consider the following loop:
do i=1,n
do i=1,m
ia(i,j)=b(i,j)+d(i,j)
isum=isum+ia(i,j)
end
end
Here, we have a race due to
isum
. This race cannot be removed by the techniques discussed above. However, the
+
operation used to compute
isum
is associative and
isum
only appears in the statement that computes its value.
The integer addition operation is not really associative, but in practice we can assume it is if the numbers are small enough so there is never any overflow.
Under these circumstances, the loop can be transformed into the following form:
c$omp parallel private(local_isum)
local_isum=0
c$omp pdo
do i=1,n
do j=1,m
local_isum=local_isum + ia(j,i)
end do
end do
c$omp end pdo nowait
c$omp critical
isum=isum+local_isum
c$omp end critical
c$omp end parallel
Here, we use the critical directive to avoid the following problem.
The statement
isum=isum+local_isum
will be translated into a machine language sequence similar to the following:
load register_1,isum
load register_2,local_isum
add register_3,register_1,register_2
store register_3,isum
Assume now there are two tasks executing the statement
isum=isum+local_isum
simultaneously. In one
local_sum
is
10
, and in the other
15
. Assume
isum
is 0 when both tasks start executing the statement. Consider the following sequence of events:
|
time
|
task 1
|
isum
|
task 2
|
|
1
|
load r1,local_isum
|
0
|
|
|
2
|
load r2, isum
|
0
|
load r1,local_isum
|
|
3
|
add r3,r2,r1
|
0
|
load r2,isum
|
|
4
|
store r3, isum
|
10
|
add r3,r2,r1
|
|
|
|
15
|
store r3,isum
|
As can be seen, interleaving the instructions between the two tasks produces incorrect results. The critical directive precludes this interleaving. Only one task at a time can execute a critical region with the same name.
The assumption is that it does not matter in which order the tasks enter a critical region as long as they are never inside a critical region of the same name at the same time.
An alternative way of writing the above parallel loop is:
c$omp parallel do reduction(+:isum)
do i=1,n
do j=1,n
isum=isum+ia(j,i)
end do
end do
The reduction clause can be applied to a number of operations and intrinsic functions.